Eine statistische Denksportaufgabe

Ich bin neulich über eine interessante kleine Frage gestolpert. Es geht um Roulette, aber die Frage lässt sich auch auf andere Situationen übertragen, in denen ein Ereignis unabhängig vom vorherigen mit immer der gleichen Wahrscheinlichkeit eintritt.

Bekanntlich gibt es beim Roulette 18 rote und 18 schwarze Zahlen und dann noch die Null, die weder rot noch schwarz ist und die dafür sorgt, dass am Ende die Bank gewinnt. Denn wer auf die richtige Farbe setzt, bekommt am Ende das doppelte seines Einsatzes. Aber leider ist die Wahrscheinlichkeit für Rot oder Schwarz nicht 50 Prozent, sondern etwas weniger, weil es eben noch die Null gibt. Die Chance auf einen Gewinn liegen deshalb nur bei 48,65 Prozent.

Nun also die Frage. Es fällt beim Roulette zum ersten Mal an diesem Abend die Null. Es könnte auch jede andere Zahl sein, aber wir nehmen hier die Null. Nun geht es um die Frage, wann die zweite Null fallen wird.

Die zweite Null wird mit größter Wahrscheinlichkeit fallen

1. beim nächsten Spiel,
2. beim 37 Spiel, da es ja 37 Zahlen gibt,
3. die Wahrscheinlichkeit für die zweite Null ist bei allen Spielen gleich.

Bei einem Test beantwortete der allergrößte Teil die Frage falsch. Sie war in der Originalform aber auch etwas unglücklicher gestellt, da dort nur nach dem nächsten Ereignis gefragt wurde. Und fast alle sagten: Die Wahrscheinlichkeit für die nächste Null ist bei allen weiteren Ereignissen gleich.

Nun ist es nicht mein Ziel, meine geneigten Leser auf Abwege zu führen, deswegen habe ich bewusst eine andere Formulierung gewählt und von der zweiten Null gesprochen, nachdem gerade das erste Mal die Null gefallen ist. Vielleicht wird so deutlicher, warum Antwort 1 die richtige ist, die zweite Null also mit der höchsten Wahrscheinlichkeit bei gleich dem nächsten Spiel fallen wird.

Natürlich ist die Wahrscheinlichkeit für eine Null bei jeder Runde die gleiche (sagt man Runde beim Roulette?), bei der nächsten Runde genauso wie 1.000 Runden später. Allerdings wird es nach 1.000 Runden vermutlich nicht mehr die zweite Null sein, wohl auch nicht mehr die dritte oder vierte, eher schon die siebenundzwangiste.

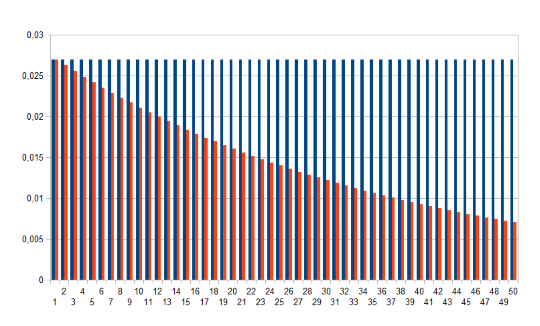
Die oberste Grafik zeigt, dass natürlich die Wahrscheinlichkeit für eine Null immer gleich ist. Wenn nicht, dann ist das Roulette-Spiel gezinkt. Aber wenn gerade die erste Null an einem Abend gefallen ist, dann ist die Wahrscheinlichkeit für die zweite Null bei gleich dem nächsten Spiel am höchsten. Sie beträgt 1/37, so hoch wie die Wahrscheinlichkeit für eine Null eben ist.

Beim übernächsten Spiel fällt ebenfalls mit 1/37 eine Null. Allerdings besteht die Möglichkeit, dass das bereits die dritte Null ist und eben nicht mehr die zweite. Es gibt also diese Möglichkeiten:

• In 36 von 37 Fällen fällt keine Null
• In einem von 37 Fällen fällt sie, davon aber wiederum
  • ist es mit einer Wahrscheinlickeit von 36/1369 die zweite Null,
  • mit einer Wahrscheinlichkeit von 1/1369 schon die dritte.

Wie kommen wir auf die 1/1369? Ganz einfach, mit einer Wahrscheinlichkeit von 1/37 fällt die Null und davon wiederum ist sie mit einer Wahrscheinlichkeit von 1/37 bereits zuvor gefallen. 37*37=1369

Das geht immer so weiter. Am einfachsten berechnen kann man die Wahrscheinlichkeit für die zweite Null, indem man berechnet, mit welcher Wahrscheinlichkeit die Null noch nie gefallen ist. Das ist (36/37) ^x (sprich 36/37 hoch x). x ist dabei die Zahl der Durchgänge, die es bereits vorher gab, ohne den mitzurechnen, bei dem die Null das erste Mal fiel. Für den ersten Durchgang ist x also 0. Und da jede Zahl hoch 0 genau 1 ist, ist die Wahrscheinlichkeit, das bisher die zweite Null noch nicht gefallen ist, ebenfalls 1 oder 100 Prozent. Das ist ja auch logisch, wie sollte sie auch.

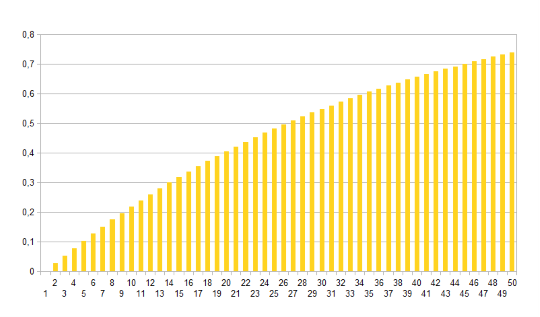
Die obige gelbe Kurve zeigt den umgekehrten Zusammenhang, also dass die Null bereits gefallen ist – als 1- (36/37) ^x . Die Gesamtwahrscheinlichkeit kann man aber besser direkt berechnen, indem man (36/37) ^x einfach noch mit 1/37 multipliziert, also der Wahrscheinlichkeit für eine Null. Denn das sind ja die beiden Bedingungen, dass

• vorher noch keine Null gefallen ist (dann ist es nicht mehr die zweite Null)
• und überhaupt eine Null fällt (sonst erübrigt sich die Diskussion, ob es vorher schon eine gab).

95 Prozent der Befragten haben diese Frage übrigens angeblich falsch beantwortet. Vermutlich deshalb, weil die Bedeutung von „die nächste“ oder „die zweite“ übersehen wurde. Ich hoffe, ich habe die erfahrenen Statistiker nicht zu sehr gelangweilt. Für die nächste Woche suche ich mir wieder eine schön Zahl, dann wird es um die Rendite der gesetzlichen Rente gehen.