Die Datenlage zu Corona ist nach wie vor schlecht. Impfbefürworter und -gegner werfen sich gegenseitig vor, mit falschen Zahlen zu arbeiten. Die unbrauchbaren Zahlen zur Corona-Inzidenz nach Impfstatus in Bayern (externer Link) beweisen für viele Impfgegner, dass man „dem Staat“ nicht glauben darf. Sie führen eine britische Statistik ins Feld, die nach der in der Altersgruppe der 10- bis unter-60-Jährigen relativ mehr ungeimpfte als geimpfte Menschen starben. Doch diese Schlussfolgerung ist vermutlich falsch. Warum widersprechen sich die Daten so häufig?
Ich möchte in diesem Beitrag nicht für oder gegen eine Impfung Stellung beziehen, wenngleich ich sagen will, dass nach den Daten, die ich kenne, alles für eine Corona-Impfung spricht. Allerdings geht es mir hier mehr darum zu erläutern, wie es sein kann, dass die britischen Daten so unterschiedlich interpretiert werden.
Spoileralarm: Nach meiner Einschätzung beweisen sie nicht, dass eine Impfung für unter 60-Jährige mehr Schaden als Nutzen bringt, man kann die These ohne weitere Daten aber auch nicht widerlegen.
Das Problem mit der Kausalität
Ein beobachteter Zusammenhang muss nicht unbedingt auf eine direkte Kausalität hindeuten. Das ist möglich, aber nicht die einzige Option. Manchmal ist die Wirkung indirekt, teilweise aber gibt es gar keine Wirkung von A auf B, sondern eine dritte Variable beeinflusst mein Ergebnis. Hier nicht aufgeführt ist noch eine vierte Option, der Zufall.
Ich möchte hier alle vier Optionen am Beispiel der Diskussion um die britischen Daten zur Übersterblichkeit Geimpfter mal durchgehen.
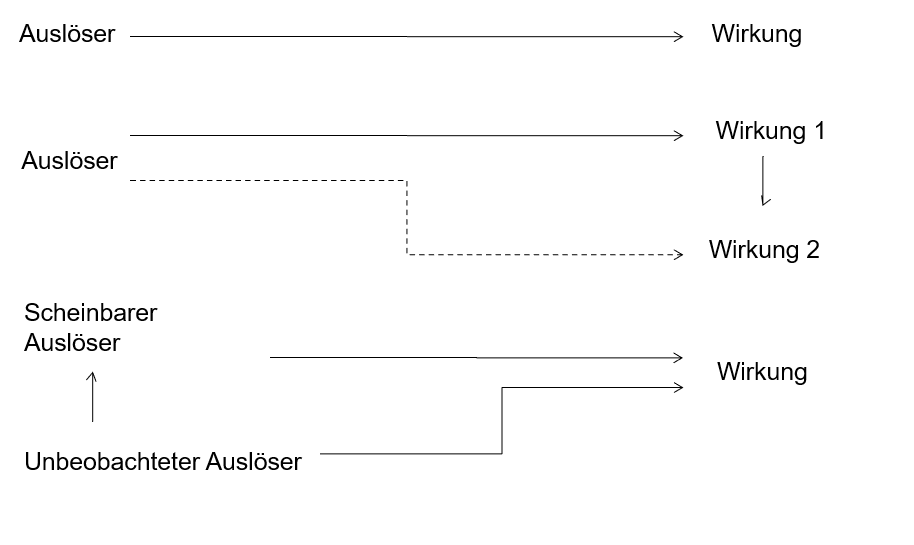
Option 1: Direkter Zusammenhang
Impfgegner argumentieren, die Impfung sei ursächlich dafür verantwortlich, dass mehr geimpfte Menschen in der Altersgruppe der 10 bis unter-60-Jährigen sterben als ungeimpfte. Ich glaube das nicht, will das aber einfach mal so stehen lassen.
Dagegen spricht, dass die Impfung in anderen Altersgruppen deutlich positive Wirkungen zeigt. Allerdings würde ich auch nicht so weit gehen wie Wulf Rohwedder von der Tagesschau, der von „gezielter Datenselektion“ spricht. Dass die Analyse von Chancen und Risiko bei der Gruppe der unter 60-Jährigen zu einem anderen Ergebnis kommt als bei den über 60-Jährigen, ist zumindest möglich. Allerdings sprechen dagegen Zahlen aus anderen Ländern.
Immerhin haben wir einen Vorteil bei unserem Thema. Wenn es einen direkten Zusammenhang zwischen der Impfung und einer tödlich verlaufenden Corona-Infektion gibt, dann führt die von der Impfung zum Tod.
Das ist nicht immer so. Wenn wir einen Zusammenhang von Armut und Krankheit feststellen, kann das sowohl bedeuten, dass Armut krank macht als auch, dass Krankheit arm macht.
Option 2: indirekter Zusammenhang
Es gibt auch noch eine weitere Option, dass der Zusammenhang nämlich ein indirekter ist. Wie könnte das in unserem Beispiel aussehen? Beispielsweise so, dass der Körper so mit der Verarbeitung der Impfung beschäftigt ist, dass er zunächst anderen Viren und Bakterien zu wenig entgegensetzen kann. Das schwächt ihn weiter und macht ihn anfällig für eine tödliche COVID-Infektion.
Das ist zugegeben etwas theoretisch und in meinen Augen nicht besonders plausibel, es geht hier aber auch zunächst um das Darstellen von Möglichkeiten, die später empirisch zu überprüfen wären.
Option 3: Scheinkausalität und Simpson-Paradoxon
Die Zahlen beweisen aber keineswegs, dass es einen direkt oder indirekten Zusammenhang zwischen der Impfung und der höheren Todesrate gibt. Vielmehr können Drittvariablen die Ursache sein. Diese Erklärung halte ich auch für die wahrscheinlichste und dabei kommt ein Phänomen ins Spiel, das als Simpson-Paradoxon bezeichnet wird.
Damit ist gemeint, dass sich im Gesamtergebnis ein Effekt zeigt, der sich umkehrt, sobald man Teilgruppen betrachtet. In unserem Fall wären das Altersgruppen, die etwas enger fasst sind als die große der 10- bis unter-60-Jährigen.
Im Beispiel überleben geimpfte Menschen in beiden betrachteten Altersgruppen häufiger als ungeimpfte, sterben aber insgesamt häufiger. Warum? Weil sie in der stärker betroffenen Altersgruppe der 60 bis unter-60-Jährigen relativ häufiger vorkommen.
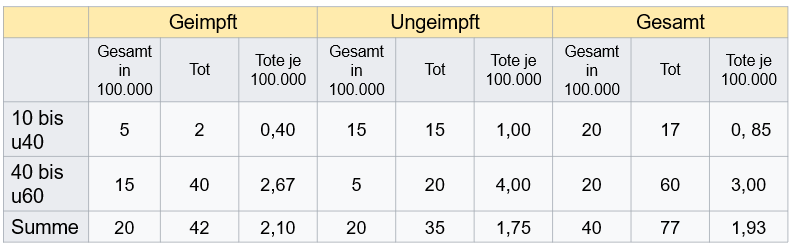
Die Zahlen sind erfunden, doch einen ähnlichen Effekt könnte es auch in der Realität geben. Tatsächlich zeigen Daten aus den USA, dass dort sowohl in der Altersgruppe der 18 bis unter 30-Jährigen (andere Altersstruktur als im Vereinigten Königreich) als auch bei den 30 bis unter 50-Jährigen relativ mehr ungeimpfte als geimpfte Menschen sterben und gleichzeitig die Sterbewahrscheinlichkeit in der höheren Altersgruppe deutlich höher ist.
Leider fehlen mir Daten, die für Großbritannien und Nordirland die Impfrate nach Alter aufschlüsseln. Trotzdem ist diese Hypothese mein persönlicher Favorit.
Es sind auch noch weitere Optionen denkbar, beispielsweise dass sich Menschen mit Vorerkrankungen häufiger impfen lassen.
Option 4: der Zufall
Es gibt natürlich noch eine vierte Option, nämlich den Zufall. In der Altersgruppe der unter 60-Jährigen sterben erfreulicherweise nicht so viele Menschen. Deshalb kann dort der Zufall eine relevante Rolle spielen.
Fazit
Mein Favorit für die Erklärung der überraschenden Zahlen im Vereinigten Königreich ist ein Simpson-Paradoxon. Das wäre jetzt empirisch zu überprüfen. Es ist leider zu einfach nur zu sagen, wir haben doch eine Erklärung gefunden, die das paradoxe Ergebnis erklärt, damit ist alles gut. Wir müssen sie auch empirisch untermauern und idealerweise die ersten beiden Optionen widerlegen.
Hallo,
@MV: Das Simpson-Parodox kann man leicht durch eine Doppelblindstudie und/oder dem Arbeiten mit statistischen Zwillingen vermeiden. Das wurde aber nicht richtig gemacht. So wurden bei beiden mRNA-Impfstoffen die Kontrollgruppen entblindet und nachgeimpft. Das ist so einfach Pfusch.
Es gibt dann auch noch einen weiteren Effekt durch die Zählweise. Bis weniger als zwei Wochen nach der zweiten Impfung werden die „Impflinge“ als Ungeimpfte gezählt. Falls also die Impfung zu einem schnellen Ableben führt, sind die Toten über alle Ursachen dadurch bei den Ungeimpften durch die Teilgeimpften erhöht.
Ich bleibe bei meiner Kritik an den Daten. Ungeimpfte und Geimpfte sind nicht alle Gruppen, die man betrachten muss. Es fehlen die Teilgeimpften und natürlich die mit dem Impfstatus unbekannt. Daher sind alle Versuche mit einem Vierfeld Vergleiche anzustellen sinnlos. Man kann sich aber mit einer einfachen Zeitreihenanalyse an das Thema nähern. Und dann wird es wieder interessant. Man sieht einen kurzen Peak bei der Sterberate der Ungeimpften in den Daten. Dieser Peak tritt in den jeweiligen Altersgruppen immer kurz nach dem Beginn der Impfungen in dieser Altergruppe auf. Das deutet auf ein Sterben der „Impflinge“ in dem Zeitraum bis kurz vor den zwei Wochen hin, in dem diese noch als Ungeimpfte gezählt werden.
Das im BBC-Bericht erwähnte extrem breite Altersintervall für die Menschen im typischerweise erwerbstätigen Alter ist natürlich Pfusch. Nicht umsonst hat sich bei den ernsthaften Statistiken die Einteilung in 10er-Gruppen durchgesetzt. Diese ist relativ unempfindlich gegen dieses Simpson-Parodox.
Bei den Daten des RKI über die Auslastungen der Notfallstationen SUMO Situationsreport wird über 20er-Gruppen gerechnet. Das ist auch schon brauchbar. Und da sieht man bei den Gruppen 0 bis 19 und 20 bis 39 nach dem Beginn der Impfungen in diesen Altersklassen einen Anstieg der Einweisungen in diesen Altersklassen. Aber Vorsicht beim Interpretieren dieser Daten. Irgendwann mal im Dezember 2021 sanken die Zahlen überraschen und unerwartet rückwirkend in den Diagrammen. Einfach mal durchs Archiv stöbern. Hier die Daten:
RKI – Fachgebiet 32 Surveillance | ÖGD-Kontaktstelle – Routinedaten aus dem Gesundheitswesen in Echtzeit (SUMO)
https://www.rki.de/DE/Content/Institut/OrgEinheiten/Abt3/FG32/sumo/sumo.html
Mit dem Beginn der Impfungen in einer Altergruppe traten besonders bei den Jungen vermehrt Einweisungen in die Notaufnahmen statt. Diese Korrelation ist verdächtig. Diese Korrelation taucht auch in den Daten aus GB/England bzgl. der Toten über alle Ursachen und unabhängig vom Impfstatus auf. Generell sind Rechnungen mit dem Imfpstatus sehr fehleranfällig. Das liegt an der unsauberen und unvollständigen Erfassung, häufig auch ohne ausreichende Abstufung.
Eine Korrelation ist keine Kausalität. Aber eine Kausalität drückt sich in einer Korrelation aus. Und die Kausalität einer Schutzwirkung der Impfungen sehe ich nicht in den Korrelationen jenseits der unbrauchbaren Vergleiche über den Impfstatus. Ich sehe da bei Infekionsgeschene und Sterblichkeit ohne Berücksichtigung des Impfstatus Korrelationen die sich besser mit einer Schad- als Nutzwirkung vertragen.
Option 1 wäre der Effekt der antivirus dependend enhancement (ADE). Das wurde bei einigen Viren und bei relativ wenigen Impfungen schon beobachtet. Die Zulassungsstudien lassen keine Aussagen über die Abwesenheit dieses Effekts zu, da diese mit viel zu wenigen Infektionen in Test- und Kontrollgruppe durchgeführt wurden.
Die Option 2 kennt man von der Influenzaschutzimpfung. Dort wird dieses Verhalten mal als vaccine associated hypersensivity und mal als virus interference bezeichnet. Die Untersuchungen sind da nicht ganz übereinstimmend, aber im Großen und Ganzen kommt da eine Schutzquote von Null raus. Mal eine schwarze und mal eine rote Null. Daher kann diese Option nicht ausgeschlossen werden und muss als realistisch und wahrscheinlich betrachtet werden.
Die Spitzenreiter unter den ARE-Viren (akute respiratorische Erkrankung) durchseuchen in einer Saison rund 10% der Bevölkerung in Deutschland. Die Saison fängt nach Kalenderwoche KW 40 an und endet im Folgejahr vor KW 20. Insgesamt werden 200% der Bevölkerung durchseucht. Das bedeutet im Schnitt zwei Infektionen pro Jahr. Das sind die längjährigen Erfahrungen mit saisonalen ARE. Damit kann man die Eintreffwahrscheinlichkeiten für ADE raten. VAH ist sehr viel schwieriger, da vorab nicht bekannt ist welche Viren VAH auslösen. Bei der Influenzaschutzimpfung macht diese etwa 5% aller Infektionen, hat im Mittel gegen die Influenza eine Schutzquote von 30% (nach Angaben der Arbeitsgemeinschaft Influenza (AGI) des RKI) und die Überempfindlichkeit besteht dann gegen hCoV (verschiedene andere Quellen), welche mindestens das Doppelte an Infektionen machen. Daher auch die Schutzquote Null.
RKI (Arbeitsgemeinschaft Influenza): Saisonberichte
https://influenza.rki.de/Saisonbericht.aspx
Noch ein kleiner Einschub: Die Spitzenreiter unter den Viren schaffen es zu ihren besten Zeiten rund 1% der Bevölkerung in der Woche zu durchseuchen. Das entspricht einer 7-Tage-Inzidenz von 1000. Das sind also keine so extremen Werte. Inzidenzen von 1000 sind das alte Normal. Das wurde für die Influenza beobachtet und die Nahverkehrsstudie aus FfM hat dies auch für nCoV-2019 gezeigt. U. a. aus diesem Grund hat die WHO auch für die Influenza die Kontaktverfolgung nicht empfohlen.
Ich betrachte Option 1 als möglich und Option 2 als ziemlich sicher gegeben. Nur die Quantifizierung ist problematisch.
Option 3 Zufall kann man erweitern. Das Wetter ist ein bestimmender Faktor für diese (behüllte) Viren. Sommer und Herbst 2020 waren wesentlich virenfeindlicher als Sommer und Herbst 2021. Das spielt auch eine große Rolle. Einstieg in die Problematik findet man in:
The Transmission of Epidemic Influenza
Authors: Hope-Simpson, R.E. © 1992
https://www.springer.com/gp/book/9780306440731
Leider ist der meteorologische Teil im Buch aus der Sicht eines Diplom Wetterfrosch etwas unterbelichtet. Die aktuelle Großwetterlage deutet auf eine hohe Chance auf einen echten™ Winter bis in den März 2022 hin. Falls dies eintritt werden die Zahlen unschön werden.
Option 4 ist irgendwie „Was nicht sein darf, kann nicht sein!“?
Der Ansatz zur Erfassung der Menschen ist schon vollkommen falsch. Es gibt nicht einfach nur „Geimpft“ und „Ungeimpft“. Es gibt mindestens 4 relevante Gruppen zur Erfassung.
* Status Ungeimpft
* Status Teilgeimpft
* Status Vollgeimpft
* Status Unbekannt
Bei den alten „Rechnungen“ des RKI wurden aber Teilgeimpfte und Unbekannte den Ungeimpften zugeschlagen. Das ist Unsinn gewesen. Jetzt werden die Unbekannten aus der Rechnung geworfen. Das ist aber ein beliebter Einstieg in Statistikbetrug. Beispiele kenne ich seit vielen Jahrzehnten aus ganz anderen Bereichen und bin immer wieder darüber erstaunt wie viele Menschen darauf rein fallen. Besonders auffällig ist da das Wachsen der Unbekannten in den letzten Wochen. Die Zahlen des RKI sind also unseriös und können nicht als Argument für die Impfungen herangezogen werden. Die britischen Messungen sehen etwas besser aus, lassen aber auch keine eindeutigen Aussagen pro Impfung zu. Wäre die Impfung so gut, müsste nicht für diese manipuliert werden. Das widerum spricht gegen die Impfung. Manipulierte Daten sind immer ein Warnzeichen! Pfoten weg! Das ist unseriös.
Dazu der ausgezeichnete BBC podcast „More or Less“ …
Podcast/Article:
Simpson’s Paradox: How to make vaccinated death figures misleading
URL:
http://open.live.bbc.co.uk/mediaselector/6/redir/version/2.0/mediaset/audio-nondrm-download/proto/http/vpid/p0b6j0x4.mp3
Description:
Vaccines are the best way to stop deaths and serious cases related to covid19, this is an irrefutable fact. However, recent ONS data seems to show that vaccinated people had a higher all cause death rate than unvaccinated people. Why is this data misleading? Here’s a clue: it’s to do with a quirky statistical phenomenon called Simpsons Paradox.
(Image: The Simpsons / TCFFC )
This content comes from:
More or Less: Behind the Stats
URL:
http://downloads.bbc.co.uk/podcasts/radio4/moreorless/rss.xml